Podemos clasificar las funciones atendiendo a la relación que guardan entre sí los elementos del dominio, del codominio y de la imagen. En este apartado veremos dicha clasificación, particularizando para el caso de las funciones reales:
Antes de ir a por ello, es bueno que recuerdes:
-
Una función es una relación entre dos conjuntos en la que a cada elemento del primer conjunto le corresponde un único elemento del segundo conjunto
-
En la definición formal de función se da el conjunto inicial, denominado dominio, el conjunto final, denominado codominio, y la regla de correspondencia entre ellos. Por ejemplo, en:
El dominio es el conjunto de los números naturales,ℕ , el codominio es el conjunto de los números reales, ℝ ,y la regla de correspondencia es f(n)=πn.
-
El conjunto imagen o recorrido de la función es el subconjunto del codominio formado por los valores que realmente toma la función, una vez se aplica a los elementos del conjunto inicial o dominio. En el caso del ejemplo anterior sería el subconjunto de los reales y que se obtienen al aplicar, a cada número natural n, y=πn.
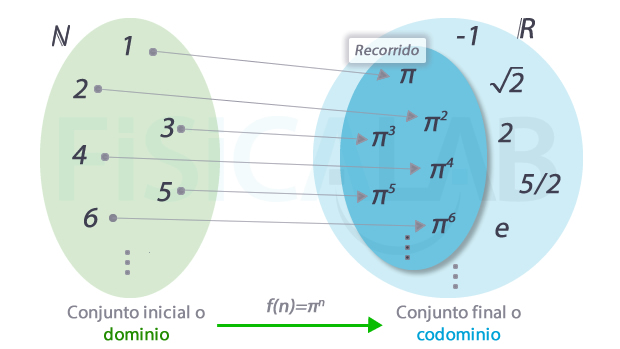 Dominio, codominio y recorrido de una función
En la función de nuestro ejemplo, el dominio es el conjunto formado por todos los números naturales. Aunque en ocasiones se confunden, observa la diferencia entre el codominio, formado por todos los reales, y el recorrido, un subconjunto de este cuyos valores cumplen la regla de correspondencia.
Dominio, codominio y recorrido de una función
En la función de nuestro ejemplo, el dominio es el conjunto formado por todos los números naturales. Aunque en ocasiones se confunden, observa la diferencia entre el codominio, formado por todos los reales, y el recorrido, un subconjunto de este cuyos valores cumplen la regla de correspondencia.
-
En una función real de variable real el dominio y el codominio (y por tanto el recorrido) son subconjuntos de los números reales
Podemos clasificar las funciones atendiendo a la relación que guardan entre sí los elementos del dominio, del codominio y de la imagen. En este apartado veremos dicha clasificación, particularizando para el caso de las funciones reales:
Antes de ir a por ello, es bueno que recuerdes:
- Una función es una relación entre dos conjuntos en la que a cada elemento del primer conjunto le corresponde un único elemento del segundo conjunto
- En la definición formal de función se da el conjunto inicial, denominado dominio, el conjunto final, denominado codominio, y la regla de correspondencia entre ellos. Por ejemplo, en:
El dominio es el conjunto de los números naturales,ℕ , el codominio es el conjunto de los números reales, ℝ ,y la regla de correspondencia es f(n)=πn. - El conjunto imagen o recorrido de la función es el subconjunto del codominio formado por los valores que realmente toma la función, una vez se aplica a los elementos del conjunto inicial o dominio. En el caso del ejemplo anterior sería el subconjunto de los reales y que se obtienen al aplicar, a cada número natural n, y=πn.
 Dominio, codominio y recorrido de una funciónEn la función de nuestro ejemplo, el dominio es el conjunto formado por todos los números naturales. Aunque en ocasiones se confunden, observa la diferencia entre el codominio, formado por todos los reales, y el recorrido, un subconjunto de este cuyos valores cumplen la regla de correspondencia.
Dominio, codominio y recorrido de una funciónEn la función de nuestro ejemplo, el dominio es el conjunto formado por todos los números naturales. Aunque en ocasiones se confunden, observa la diferencia entre el codominio, formado por todos los reales, y el recorrido, un subconjunto de este cuyos valores cumplen la regla de correspondencia. - En una función real de variable real el dominio y el codominio (y por tanto el recorrido) son subconjuntos de los números reales
Funciones inyectivas
Una función es inyectiva cuando no hay dos elementos del dominio que tengan la misma imagen. Formalmente:
Es decir, para cualesquiera dos elementos a y b, pertenecientes al dominio de la función Domf, si sus imágenes f(a) y f(b) son iguales, los elementos son necesariamente iguales.
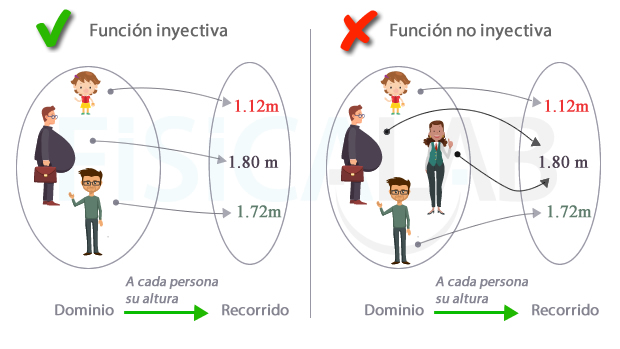 Inyectiva vs no inyectiva
A la izquierda, una función que asocia a cada persona su altura. A cada elemento del recorrido llega una sola flecha, por lo que la función es inyectiva. A la derecha, la función también asocia a cada persona su altura. En este caso el dominio es ligeramente distinto, y cuenta con una persona más que, curiosamente, tiene la misma altura que el oficinista despreocupado de su peso (1.80m). Como a ese elemento del recorrido llegan dos flechas, la función ya no es inyectiva.
Por tanto, si te piden una demostración de que una función no es inyectiva, puedes hallar dos valores distintos del dominio cuyas imágenes sean iguales. Si las encuentras, la función no es inyectiva.
En el caso de funciones reales, para saber si son inyectivas:
Inyectiva vs no inyectiva
A la izquierda, una función que asocia a cada persona su altura. A cada elemento del recorrido llega una sola flecha, por lo que la función es inyectiva. A la derecha, la función también asocia a cada persona su altura. En este caso el dominio es ligeramente distinto, y cuenta con una persona más que, curiosamente, tiene la misma altura que el oficinista despreocupado de su peso (1.80m). Como a ese elemento del recorrido llegan dos flechas, la función ya no es inyectiva.
Por tanto, si te piden una demostración de que una función no es inyectiva, puedes hallar dos valores distintos del dominio cuyas imágenes sean iguales. Si las encuentras, la función no es inyectiva.
En el caso de funciones reales, para saber si son inyectivas:
-
Cuando están dadas mediante una ecuación, podemos utilizar la propia definición. Así, la función f(x)=2·x+1 es inyectiva, pues:
Por otro lado, la función f(x)=x2 no es inyectiva pues:
-
Cuando están dadas gráficamente se trata de buscar dos imágenes iguales en la misma. Observa la siguiente ilustración y lo entenderás más claramente:
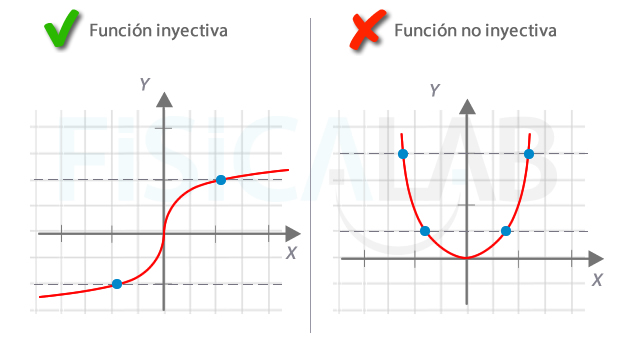 Gráficas de funciones inyectivas
A la izquierda, una función real inyectiva, frente a una que no lo es, a la derecha. La prueba para determinar si una función real es inyectiva, a partir de su gráfica, consiste en buscar una recta horizontal que pueda cortar a la gráfica en más de un punto. Si la encuentras, como en el caso de la gráfica derecha, la función no es inyectiva. Si no existe ninguna recta así, como en el caso de la izquierda, la función es inyectiva. En cada gráfica se han utilizado dos rectas de prueba.
Gráficas de funciones inyectivas
A la izquierda, una función real inyectiva, frente a una que no lo es, a la derecha. La prueba para determinar si una función real es inyectiva, a partir de su gráfica, consiste en buscar una recta horizontal que pueda cortar a la gráfica en más de un punto. Si la encuentras, como en el caso de la gráfica derecha, la función no es inyectiva. Si no existe ninguna recta así, como en el caso de la izquierda, la función es inyectiva. En cada gráfica se han utilizado dos rectas de prueba.
No debes confundir la prueba de la recta vertical, utilizada para saber si una gráfica corresponde a una función, con la prueba de la recta horizontal, utilizada para saber si una función es inyectiva.
Una función es inyectiva cuando no hay dos elementos del dominio que tengan la misma imagen. Formalmente:
Es decir, para cualesquiera dos elementos a y b, pertenecientes al dominio de la función Domf, si sus imágenes f(a) y f(b) son iguales, los elementos son necesariamente iguales.

Inyectiva vs no inyectiva
A la izquierda, una función que asocia a cada persona su altura. A cada elemento del recorrido llega una sola flecha, por lo que la función es inyectiva. A la derecha, la función también asocia a cada persona su altura. En este caso el dominio es ligeramente distinto, y cuenta con una persona más que, curiosamente, tiene la misma altura que el oficinista despreocupado de su peso (1.80m). Como a ese elemento del recorrido llegan dos flechas, la función ya no es inyectiva.
Por tanto, si te piden una demostración de que una función no es inyectiva, puedes hallar dos valores distintos del dominio cuyas imágenes sean iguales. Si las encuentras, la función no es inyectiva.
En el caso de funciones reales, para saber si son inyectivas:
- Cuando están dadas mediante una ecuación, podemos utilizar la propia definición. Así, la función f(x)=2·x+1 es inyectiva, pues:
Por otro lado, la función f(x)=x2 no es inyectiva pues: - Cuando están dadas gráficamente se trata de buscar dos imágenes iguales en la misma. Observa la siguiente ilustración y lo entenderás más claramente:
 Gráficas de funciones inyectivasA la izquierda, una función real inyectiva, frente a una que no lo es, a la derecha. La prueba para determinar si una función real es inyectiva, a partir de su gráfica, consiste en buscar una recta horizontal que pueda cortar a la gráfica en más de un punto. Si la encuentras, como en el caso de la gráfica derecha, la función no es inyectiva. Si no existe ninguna recta así, como en el caso de la izquierda, la función es inyectiva. En cada gráfica se han utilizado dos rectas de prueba.
Gráficas de funciones inyectivasA la izquierda, una función real inyectiva, frente a una que no lo es, a la derecha. La prueba para determinar si una función real es inyectiva, a partir de su gráfica, consiste en buscar una recta horizontal que pueda cortar a la gráfica en más de un punto. Si la encuentras, como en el caso de la gráfica derecha, la función no es inyectiva. Si no existe ninguna recta así, como en el caso de la izquierda, la función es inyectiva. En cada gráfica se han utilizado dos rectas de prueba.
No debes confundir la prueba de la recta vertical, utilizada para saber si una gráfica corresponde a una función, con la prueba de la recta horizontal, utilizada para saber si una función es inyectiva.
Ejemplos
F. inyectiva F. no inyectiva
| F. inyectiva | F. no inyectiva |
|---|---|
Funciones sobreyectivas
Una función es sobreyectiva, también llamada suprayectiva o exhaustiva, cuando el codominio y el recorrido coinciden. Formalmente:
Es decir, para cualquier elemento y del codominio existe otro elemento x del dominio tal que y es la imagen de x por f.
Las funciones reales son sobreyectivas cuando Recf=ℝ, ya que, por definición, en ellas Codf=ℝ.
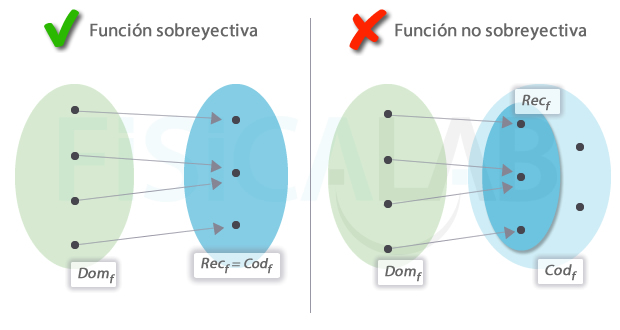 Sobreyectiva vs no sobreyectiva
A la izquierda, una función sobreyectiva. Como tal, el codominio y el recorrido coinciden. O, dicho de manera más gráfica, todos los elementos del codominio reciben flechas. A la derecha, una función no sobreyectiva. En este caso hay elementos del codominio que no están incluidos en el recorrido. Observa, además, que ambas funciones son no inyectivas, pues ambas cuentan con elementos en el recorrido que reciben más de una flecha.
Por tanto, si te piden una demostración de que una función real es sobreyectiva, puedes hallar la imagen de dicha función. Si la imagen es el conjunto de los reales, la función es sobreyectiva. En caso contrario, no.
Sobreyectiva vs no sobreyectiva
A la izquierda, una función sobreyectiva. Como tal, el codominio y el recorrido coinciden. O, dicho de manera más gráfica, todos los elementos del codominio reciben flechas. A la derecha, una función no sobreyectiva. En este caso hay elementos del codominio que no están incluidos en el recorrido. Observa, además, que ambas funciones son no inyectivas, pues ambas cuentan con elementos en el recorrido que reciben más de una flecha.
Por tanto, si te piden una demostración de que una función real es sobreyectiva, puedes hallar la imagen de dicha función. Si la imagen es el conjunto de los reales, la función es sobreyectiva. En caso contrario, no.
Otra clasificación de las funciones, son las funciones inyectivas, sobreyectrivas y biyectivas, las cuáles nos dan información acerca del comportamiento de las mismas.
Recuerda que en una función, siempre tenemos un conjunto de partida (dominio), un conjunto de llegada (contradominio), y un rango:
Una función es sobreyectiva, también llamada suprayectiva o exhaustiva, cuando el codominio y el recorrido coinciden. Formalmente:
Es decir, para cualquier elemento y del codominio existe otro elemento x del dominio tal que y es la imagen de x por f.
Las funciones reales son sobreyectivas cuando Recf=ℝ, ya que, por definición, en ellas Codf=ℝ.

Sobreyectiva vs no sobreyectiva
A la izquierda, una función sobreyectiva. Como tal, el codominio y el recorrido coinciden. O, dicho de manera más gráfica, todos los elementos del codominio reciben flechas. A la derecha, una función no sobreyectiva. En este caso hay elementos del codominio que no están incluidos en el recorrido. Observa, además, que ambas funciones son no inyectivas, pues ambas cuentan con elementos en el recorrido que reciben más de una flecha.
Por tanto, si te piden una demostración de que una función real es sobreyectiva, puedes hallar la imagen de dicha función. Si la imagen es el conjunto de los reales, la función es sobreyectiva. En caso contrario, no.
Otra clasificación de las funciones, son las funciones inyectivas, sobreyectrivas y biyectivas, las cuáles nos dan información acerca del comportamiento de las mismas.
Recuerda que en una función, siempre tenemos un conjunto de partida (dominio), un conjunto de llegada (contradominio), y un rango:
Función inyectiva
Una función es inyectiva si cada elemento del conjunto de llegada corresponde como máximo a un elemento del conjunto de partida.
Otra definición es la siguiente: una función f: A -> B es inyectiva, si no existen 2 elementos de A (conjunto de llegada) con una misma imagen. Veamos algunos ejemplos:
 Para determinar si una función es inyectiva, tenemos que analizar la siguiente condición:
Para determinar si una función es inyectiva, tenemos que analizar la siguiente condición:
Una función es inyectiva si cada elemento del conjunto de llegada corresponde como máximo a un elemento del conjunto de partida.
Otra definición es la siguiente: una función f: A -> B es inyectiva, si no existen 2 elementos de A (conjunto de llegada) con una misma imagen. Veamos algunos ejemplos:

Para determinar si una función es inyectiva, tenemos que analizar la siguiente condición:
Función sobreyectiva
Una función es sobreyectiva si cada elemento del conjunto de llegada (contradominio) corresponde por lo menos a un elemento del conjunto de partida.
Otra definición más simple es la siguiente: una función es sobreyectiva si el rango es igual al conjunto de llegada o contradominio. Veamos algunos ejemplos:
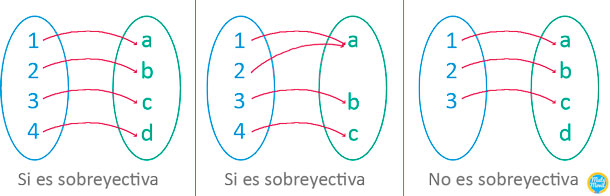 Para determinar si una función es sobreyectiva tenemos que determinar el rango. Por lo general, el conjunto de llegada es dato del problema. Si el rango que hemos hallado, es igual al conjunto de llegada, entonces se trata de una función sobreyectiva.
Para determinar si una función es sobreyectiva tenemos que determinar el rango. Por lo general, el conjunto de llegada es dato del problema. Si el rango que hemos hallado, es igual al conjunto de llegada, entonces se trata de una función sobreyectiva.
Una función es sobreyectiva si cada elemento del conjunto de llegada (contradominio) corresponde por lo menos a un elemento del conjunto de partida.
Otra definición más simple es la siguiente: una función es sobreyectiva si el rango es igual al conjunto de llegada o contradominio. Veamos algunos ejemplos:

Para determinar si una función es sobreyectiva tenemos que determinar el rango. Por lo general, el conjunto de llegada es dato del problema. Si el rango que hemos hallado, es igual al conjunto de llegada, entonces se trata de una función sobreyectiva.
Función biyectiva
Una función “f” es biyectiva si es inyectiva y sobreyectiva.
Otra definición es la siguiente: una función es biyectiva si cada elemento del conjunto de partida tiene una imagen distinta en el conjunto de llegada, y cada elemento del conjunto de llegada corresponde a un elemento del conjunto de partida.
Una función “f” es biyectiva si es inyectiva y sobreyectiva.
Otra definición es la siguiente: una función es biyectiva si cada elemento del conjunto de partida tiene una imagen distinta en el conjunto de llegada, y cada elemento del conjunto de llegada corresponde a un elemento del conjunto de partida.

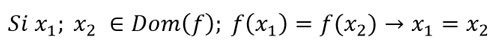
Se paso ahí profesor waooo
ResponderEliminarTodo esto hay q hacer ufff
ResponderEliminarwaoooo pero que cómodo es usted, con maestros así se llega lejos jajjaj.
ResponderEliminarYo no entiendo nada de lo que ahy que aser aqui
ResponderEliminarWao es mucho con demasiado 🥵🥵
ResponderEliminar